
Trygonometria stanowi nieodłączny element matematyki szkolnej, a umiejętność posługiwania się tablicami trygonometrycznymi jest kluczowa dla rozwiązywania zadań egzaminacyjnych. Znajomość metod odczytywania wartości funkcji trygonometrycznych oraz interpretacji danych z tablic pozwala sprawnie wykonywać obliczenia związane z miarami kątów i długościami boków w trójkątach prostokątnych.
Najważniejsze wnioski
- Tablice trygonometryczne zawierają wartości dla kątów od 0° do 90° z dokładnością do czterech miejsc po przecinku
- Sinus i tangens odczytuje się z lewej kolumny (oznaczonej α), natomiast cosinus z prawej kolumny (β)
- Przed wyszukaniem kąta należy zawsze przekształcić ułamek zwykły na dziesiętny
- Na egzaminie maturalnym uczniowie mają dostęp do oficjalnych tablic CKE, więc nie trzeba zapamiętywać wszystkich wartości
- Najczęstszym błędem jest mylenie kolumn przy odczytywaniu różnych funkcji trygonometrycznych
Czym jest trygonometria i dlaczego jest ważna?
Trygonometria to dział matematyki badający zależności między długościami boków a miarami kątów wewnętrznych w trójkątach. Nazwa tego obszaru matematyki pochodzi od greckich słów „tria” (trzy) i „gonia” (kąt), co doskonale odzwierciedla jej charakter. Ta dziedzina umożliwia pomiar rzeczywistych wielkości przy użyciu prostych narzędzi jak miarka i kątomierz. Bez znajomości zasad trygonometrii nie moglibyśmy dokładnie obliczyć wysokości drzewa lub szerokości rzeki mając jedynie podstawowe przyrządy pomiarowe. Kluczowe terminy związane z tym działem matematyki to stosunki boków, trójkąt prostokątny oraz funkcje trygonometryczne.
Zastosowania trygonometrii w życiu codziennym
Trygonometria znajduje zastosowanie w budownictwie podczas obliczania wysokości budynków i projektowania konstrukcji. Geodeci wykorzystują ją do wykonywania precyzyjnych pomiarów terenowych, astronomowie zaś do określania odległości między ciałami niebieskimi. Współczesna technologia również korzysta z tej dziedziny matematyki – nawigacja GPS oraz przetwarzanie sygnałów, w tym kompresja muzyki w formacie mp3, opierają się na funkcjach trygonometrycznych. Praktyczny przykład to pomiar wysokości drzewa: wystarczy znaleźć punkt A, zmierzyć odległość od drzewa (AB) oraz kąt α, a następnie obliczyć wysokość jako AB × tg α. Dzięki takim metodom możemy wykonywać skomplikowane pomiary mając jedynie podstawowe narzędzia.
Podstawowe funkcje trygonometryczne
Matematyka operuje czterema podstawowymi funkcjami trygonometrycznymi, które są niezbędne do rozwiązywania zadań. Oto te funkcje:
- Sinus (sin)
- Cosinus (cos)
- Tangens (tg)
- Cotangens (ctg)
Dla kąta ostrego α w trójkącie prostokątnym definicje przyjmują następującą postać: sin α to stosunek przyprostokątnej naprzeciw kąta do przeciwprostokątnej, cos α to stosunek przyprostokątnej przyległy do kąta do przeciwprostokątnej, natomiast tg α to stosunek przyprostokątnej naprzeciw kąta do przyprostokątnej przyległej. Istotną zasadą jest to, że sinus i tangens odczytujemy z lewej kolumny tabeli, a cosinus z prawej kolumny. Wizualizacja tych relacji na schemacie trójkąta prostokątnego z oznaczonymi bokami i kątami pomaga w pełnym zrozumieniu definicji.
Budowa tablic trygonometrycznych
Tablice trygonometryczne zawierają wartości funkcji dla kątów od 0° do 90° z dokładnością do czterech miejsc po przecinku. Struktura tablic opiera się na podziale na dwie kolumny: lewą oznaczoną jako α (dla sinusa i tangensa) oraz prawą oznaczoną jako β (dla cosinusa). Tablice te znajdują się na końcu oficjalnych tablic matematycznych CKE używanych na maturze, co zapewnia wszystkim uczniom równy dostęp do tych wartości podczas egzaminu. Konkretne przykłady wartości obejmują: dla kąta 30° sin 30° = 0,5000, cos 30° = 0,8660, tg 30° = 0,5774. Fragment rzeczywistej tablicy trygonometrycznej z zaznaczonymi kluczowymi wartościami pomaga zrozumieć jej układ i sposób interpretacji danych.
Odczytywanie wartości funkcji dla danego kąta
Proces znajdowania wartości funkcji trygonometrycznej dla danego kąta wymaga systematycznego podejścia. Należy wykonać następujące kroki:
- Zlokalizować kąt w odpowiedniej kolumnie (α dla sin i tg, β dla cos)
- Odczytać wartość z odpowiedniego wiersza
Przykład zastosowania: dla kąta 15° wartość sin 15° wynosi 0,2588, natomiast tg 15° = 0,2679. Krok po kroku można zaprezentować proces odczytywania wartości dla konkretnego kąta, na przykład 45°, zaznaczając odpowiednie miejsca w tabeli. Niektóre kąty mają „ładne” wartości (np. sin 30° = 0,5), co znacząco ułatwia zapamiętywanie i sprawdzanie poprawności obliczeń. Warto zapoznać się z technikami zapamiętywania wzorów matematycznych, aby efektywniej przyswajać te wartości.
Znajdowanie miary kąta na podstawie wartości funkcji
Proces odwrotny, czyli znajdowanie kąta na podstawie wartości funkcji, również wymaga określonej procedury. Pierwszym krokiem jest przekształcenie wartości na ułamek dziesiętny (np. 3/5 = 0,6), następnie trzeba znaleźć w tabeli najbliższą wartość, a na końcu odczytać odpowiadający kąt. Przykład ilustrujący to zagadnienie: jeśli sin α = 3/5 = 0,6, to α ≈ 37° (ponieważ sin 37° = 0,6018). Szczegółowy opis procesu poszukiwania kąta dla konkretnej wartości, na przykład cos α = 0,8660 → α = 30°, wymaga zaznaczenia, że często nie znajdziemy dokładnej wartości i musimy wybrać najbliższą dostępną. Dla cosinusa szukamy w prawej kolumnie tabeli, co jest kluczowe dla poprawnego wyniku.
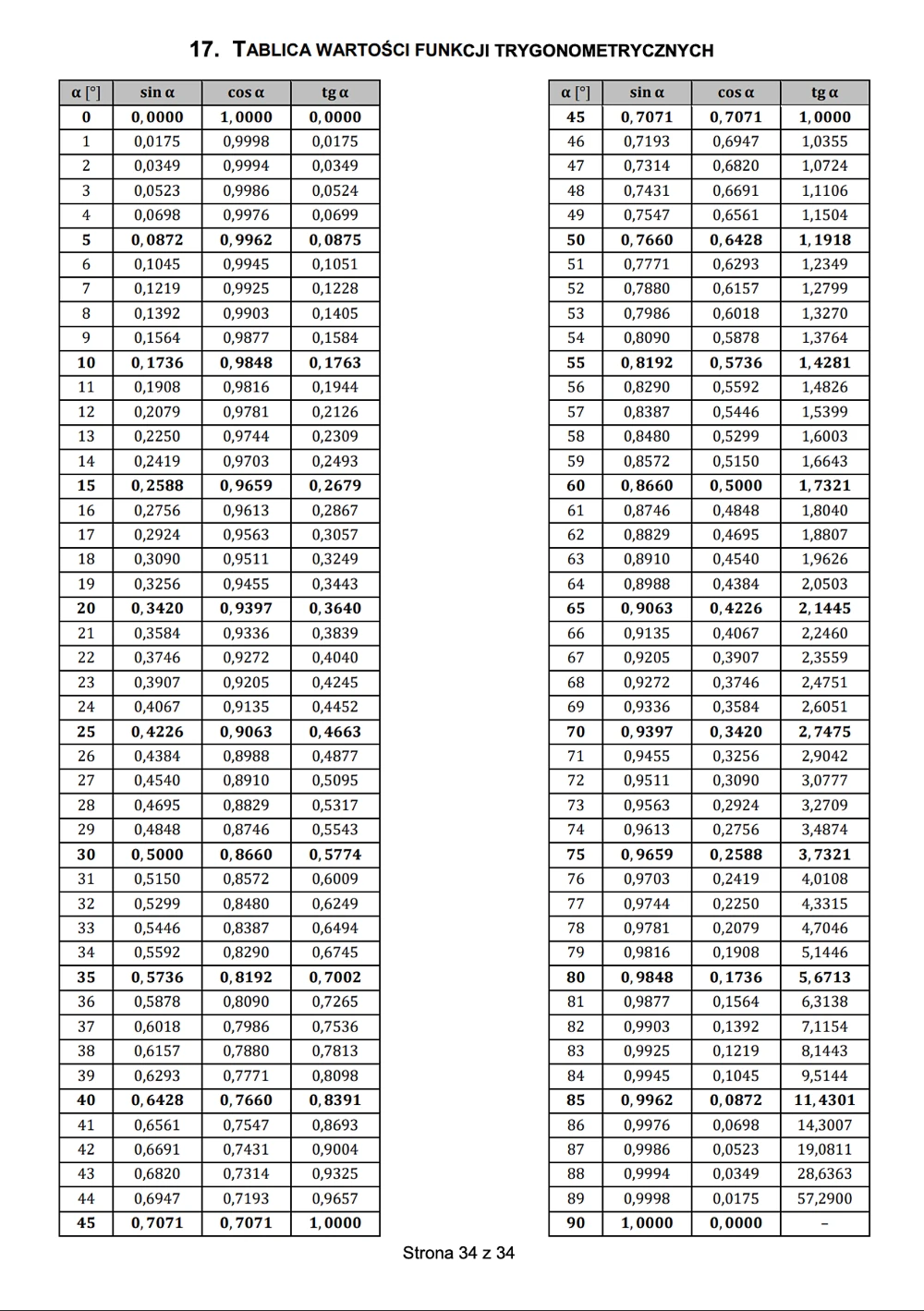
Źródło: CKE – Wzory maturalne
Rozwiązywanie typowych zadań maturalnych
Na egzaminie maturalnym często pojawiają się zadania typu: „Podaj miarę kąta α, jeśli cos α = √3/2” lub „Oblicz długość boku trójkąta znając kąt i inny bok”. Przedstawię dwa typowe zadania maturalne z pełnym rozwiązaniem krok po kroku. Zadanie pierwsze: w trójkącie prostokątnym przyprostokątna przyległa do kąta α ma długość 5 cm, przeciwprostokątna 10 cm, oblicz α. Rozwiązanie przebiega następująco: cos α = 5/10 = 0,5 → α = 60°. Na maturze uczniowie mają dostęp do tablic CKE, więc nie muszą zapamiętywać wszystkich wartości, co znacznie ułatwia pracę. Pomocne może być również zapoznanie się z wzorami maturalnymi z matematyki, aby lepiej przygotować się do egzaminu.
Najczęstsze błędy przy korzystaniu z tablic
Analizując prace uczniów, można zidentyfikować najczęstsze błędy popełniane podczas pracy z tablicami trygonometrycznymi. Typowe pomyłki obejmują:
- Mylenie kolumn
- Nieprawidłowe zaokrąglanie wartości
- Pomijanie konwersji ułamków zwykłych na dziesiętne
Przykład błędu ilustruje typową sytuację: szukając kąta dla sin α = 0,6, uczeń wybiera 36° zamiast 37°, bo nie zauważył, że 0,6018 (dla 37°) jest bliższe 0,6 niż 0,5878 (dla 36°). Dokładne odczytywanie wartości z tablic jest kluczowe dla poprawnego rozwiązania zadań i uniknięcia utraty punktów na egzaminie. W Eurokorepetycje dobieramy korepetytora do ucznia i prowadzimy zajęcia dostosowane do indywidualnego tempa i stylu nauki, co pozwala skutecznie eliminować takie błędy.
Praktyczne wskazówki dla efektywnej pracy z tablicami
Efektywna praca z tablicami trygonometrycznymi wymaga stosowania kilku kluczowych wskazówek. Zawsze najpierw przekształcaj ułamki zwykłe na dziesiętne, szukaj wartości najbliższej (nie zawsze znajdziemy dokładny odpowiednik), a także pamiętaj o odpowiedniej kolumnie dla każdej funkcji. Przydatna checklista do systematycznej pracy wygląda następująco:
⬜ Określ, jaką funkcję trygonometryczną masz podaną
⬜ Przekonwertuj na ułamek dziesiętny
⬜ Wybierz odpowiednią kolumnę tabeli
⬜ Znajdź najbliższą wartość
⬜ Odczytaj kąt
Dla kątów powyżej 45° warto korzystać z tożsamości trygonometrycznych (np. sin(90°-α) = cos α), aby uniknąć błędów przy odczycie. Zapoznanie się z kartą wybranych wzorów z matematyki pomoże utrwalić te zasady i zwiększyć pewność podczas egzaminu.
